Section 3.5 of the User's Guide for CPO2D and CPO3D
(or proceed to chapter 4)
Further advice on extrapolating to infinity
As explained above and in many places in Help, it is often possible to improve the accuracy of a result by extrapolating the number N of segments to infinity.
The appropriate values of the exponent p in the power law N**p depends on the particular quantity being extrapolated, as shown in the following table. In general it is advisable to treat p as an empirical constant.
Values of the exponent p mentioned in the Help menu:
quantity p source of information
potential, field -1.5 chapter 3, test2d01 (HDA), test3d01 (HDA)
potential, field -2 test2d15 (hole in sheet), test2d17 (mesh)
lens parameters -2 xmpl2d01,2,3,4 (lenses)
capacitance -1, -2 reference list (paper in J Comp Phys)
In practice the technique of extrapolation is usually found to be successful and reliable for 2D simulations -the plots in N**p are good straight lines- but sometimes less successful for 3D simulations.
An example of a non-smooth 3D extrapolation.
Here we present a difficult example. It is a simple simulation, but the use of the technique here is markedly less successful for 3D than 2D. It consists of a cylinder of radius 1 and length 2, plus coaxial discs of radius 1 placed at a distance of 1 from each end.
The potential of the cylinder is 0V while the two discs are at 1V. The quantity tested in the present example is the potential V0 at the centre of the cylinder.
In the computations an inaccuracy of .00001 is requested for the potential evaluations (which was the best available before 1999). In the 3D simulation the ‘iterative subdivision’ option is used with 4 stages and a ‘weight’ factor of 1.5.
A preliminary study was used to establish that the value of V0 is most sensitive to the number of subdivisions at the ends of the cylinder. The ‘concentrate subdivisions’ option (see Help) is therefore used for the ends of the cylinder, with a concentration factor of 5 (in detail, the concentration was applied to the 12 initial segments at an end length of 0.2 of the cylinder, while there were 12 segments on the rest of the cylinder and 12 on the disc, all the available reflection planes being used). The value of V0 is less sensitive to the number of subdivisions used for the middle part of the cylinder or for the discs.
The table shows the value obtained for u = (V0 - 0.065)*10000:
2D, N= 32 63 127 256 511
u= 4.18 2.95 2.34 2.15 2.11
3D, N= 36 63 96 126 192 256 384 508 768
u= 5.57 3.36 1.07 2.21 2.45 1.45 2.44 2.70 2.29
The figure shows the dependence of V0 on N**(-1.5). The solid and open circles represent 2D and 3D simulations respectively.
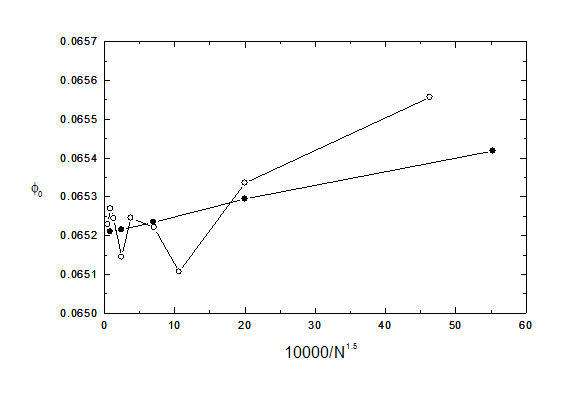
The 2D results extrapolate very well (as is usual) to 0.06521 +/- 0.00001. This uncertainty in the value is consistent with the requested inaccuracy of 0.00001. We can therefore state with some confidence that 0 = 0.06521 +/- 0.00002.
By contrast the 3D results do not extrapolate well (but see below). The three 3D results at the highest values of N are in the range 0.06523 to 0.06527, and so they differ from the accurate value by up to 0.00006, which is 6 times larger than the requested inaccuracy. The fluctuations are caused (see also below) by the fact that the sizes of the segments in the critical regions at the ends of the cylinder change unevenly as the total number N changes. The 3D extrapolation is worse than this (that is, the line is not straight for any value of the exponent p and the extrapolated value is less exact) if the ‘concentrate subdivisions’ option is not used for the ends of the cylinder. The extrapolation deteriorates further if the ‘iterative subdivision’ option is not used.
Another extrapolation technique is available that can be tried for 3D simulations when the technique described above is found to be unsatisfactory. This consists of identifying 2 or more regions and then carrying out separate extrapolations for the segments in them. In the present example one region consists of the ends of the cylinder and the other region is all the rest. The table shows the value obtained for u = (V0 - 0.065)*10000 as the numbers of segments N1 (for the ends) and N2 (for the rest) are varied.
N1= 108 108 108 108 108 27 48 108 192 432
N2= 24 96 204 384 inf 96 96 96 96 96 96
V0= -5.6 2.2 4.0 5.6 9.3(3) 7.9 5.1 2.2 0.7 -0.8 -3.7(1)
These results are displayed in the figure below, where the open and solid circles represent the values for constant N1 and N2 respectively. The appropriate (empirical) exponent for these two extrapolations is now -0.5, which gives excellent straight line fits. The extrapolations to infinity are included in the table. Using the value of V0 at N1 = 108, N2 = 96 as an ‘anchor point’, the change in going from N1 = 108 to N1 = infinity is -5.9 +/- 0.1 (that is, 2.2 to -3.7 in the table above) and the change in going from N2 = 96 to N2 = infinity is +5.7 +/- 0.3 Adding these together, the change in going to N1 = N2 = infinity is -0.2 +/- 0.3, giving u = 2.0 +/- 0.3, 0 = 0.06520 +/- 0 00003, which agrees with the value 0.06521 +/- 0.00002 given above by the 2D study.
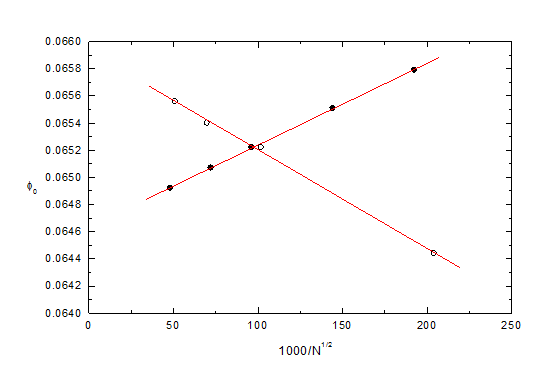
Note that in this example the two different regions have slopes of opposite sign for the extrapolations. The fluctuation behaviour of the open circles in the first figure can therefore be understood as resulting from a competition between opposing trends. Note also that when two or more regions are separately extrapolated fewer segments are required and the computing time is reduced. This is therefore a technique that should be used whenever possible.
This example therefore illustrates that when results of the highest ultimate accuracy are required in 3D simulations it is important to:
(1) carefully choose the initial distribution of subdivisions and either
(2) extrapolate the critical region separately from the rest, or
(3) use the ‘iterative subdivision’ and ‘concentrate subdivisions’ options.
Proceed to chapter 4
