Help for CPO Programs

Test3d15, 15th 'benchmark test' data file for CPO3D

Capacitance of a circular disc

The capacitance of a thin circular disc is used to illustrate the process of extrapolating the number of segments to infinity, and to illustrate the options of iterative subdivision of segments and concentration of subdivisions.

The following data were obtained when the memory and speed of PC's was much more limited than at present, so the available number of segments was small and the requested inaccuracies were fairly high to give a quick demonstration.

This is a 2-dimensional simulation, and so can be treated more accurately using CPO2D -see F H Read, J. Comp. Phys. vol 133, 1-5 (1997).

This test is included to illustrate the limitations that are sometimes encountered with the process of iterative subdivision of electrodes in 3D systems, but that can usually be overcome by the process of extrapolating different regions separately. This topic is also treated in the note on extrapolation techniques for segments. The more general topic of extrapolation is discussed in chapter 3 of the Users Guide.

The disc has a radius of 1mm, a potential of 1V and is vanishingly thin. It is known (see the above reference) that charge density is much higher near the edge of the disc than at its centre. Therefore the outer part, from r = 0.8 to 1.0, is initially divided into 16 triangles, while the inner part is divided into 8 triangles.

The initial 24 triangles are further subdivided by the program, in the present example to a total of 799 segments (as can be seen above, 800 is requested but the program achieves 799). The 'iterative subdivision' option is used. 4 stages are called for and the 'weight' factor is specified as 1.5, which for the present example seems to be more appropriate than the more usual value of 1.0.

The weight factor is entered as negative in the above data lines, which triggers the 'concentrate segments' option. The first 16 initial segments (that is, those on the outer part of the disc) are specified as the ones to be 'concentrated' and the concentration factor is 5.0. These segments are therefore treated as being 5 times more important than the others when the program is making decisions about subdividing.

Full use is made of the symmetry planes and the lowest inaccuracies are requested.

Two quantities are evaluated to test the accuracy of the calculation, the total charge Q on the disc and the potential V at r = 2, z = 0. The exact values of these are known: Q = 8.85419 10-15 (= 0*r, before the symmetry reflections), V = 1/3.

The following results are obtained as the number N of segments is increased:

Here are plots of Q and V versus 1/N:

The plot of Q versus 1/N gives a 'wobbly' fit that extrapolates to Q = 8.848 +/- 0.001, which therefore differs from the exact value by 0.07 percent.

The plot of V versus 1/N also gives a 'wobbly' fit that extrapolates to V = 0.33309 +/- 0.00004, which is therefore in error by 0.07 percent.

Both these percentages are higher than the requested inaccuracy of 0.001 percent for the potential evaluations, but are consistent with the number of segments being in the hundreds rather than thousands.

It is instructive to compare the percentage errors obtained with the highest value of N and with extrapolation:

In both cases the process of extrapolation reduces the error by a factor of approximately 2.

From the small number of other studies that have been done the indications are that this could be taken as a rough guide for other problems in which the extrapolations are not smooth. Reducing the error by a factor of 2 is equivalent to using twice as many segments when the dependence goes as 1/N, and four times as many when it is 1/N**2.

If the 'iterative subdivision' and 'concentrate segments' options are not used the results become significantly less accurate (but extrapolation still gives an approximate halving of the error).

Separate extrapolations of different regions:

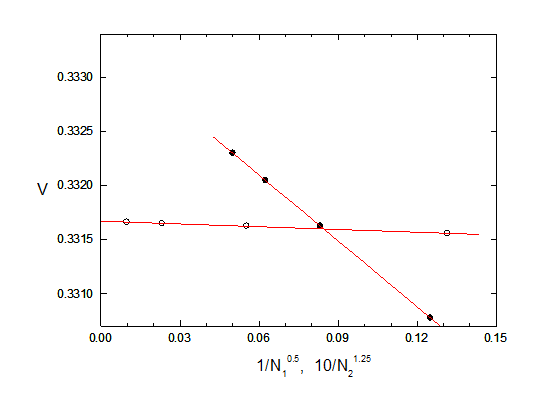
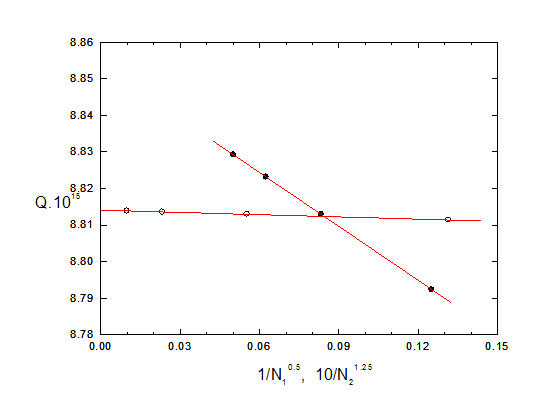
Another extrapolation technique is available however (see also the note on extrapolation techniques for segments). This consists of identifying 2 or more regions and then carrying out separate extrapolations for the segments in them. In the present example one region consists of the outer rim of the disc and the other region is all the rest. The table shows the values obtained for u = (V - 0.33)*1000 and v = Q.E17 - 880 as the numbers of segments N1 (for the rim) and N2 (for the rest) are varied.

These results are displayed in the figures below, where the solid and open circles represent the values of V and Q.E15 for variable N1 and N2 respectively. The appropriate (empirical) exponents for these extrapolations are -0.5 for N1 and -1.25 for N2, and the extrapolations to infinity are included in the table. The results are clearly more sensitive to N1 than to N2, as expected.

Using the value of u at N1 = 144, N2 = 64 as an 'anchor point', the change in u in going from N1 = 144 to N1 = infinity is -1.69+/-0.01 (that is, 1.63 to 3.32(1) in the table above) and the change in going from N2 = 64 to N2 = infinity is 0.04+/-0.01. Adding these together, the change in going to N1 = N2 = infinity is 1.73+/-0.01, giving u = 3.36+/-0.01, V = 0.33336+/-0 00001, which is near to the correct value 1/3. Similarly we find that the extrapolated value of Q is (8.855+/-0.001).E-15, which is also near to the correct value 8.853.E-15.